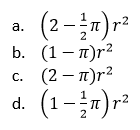PREGUNTAS TIPO ICFES: DÉCIMO-ONCE

Ejercicios grados décimo y once.

1. Una casa tiene un tanque esférico para almacenar agua, cuyo contenido alcanza para diez días. El dueño de la casa decide sustituir el tanque por otro cuyo diámetro es el doble del anterior. Determine para cuantos días alcanzará el nuevo contenido.
a. 20 días
b. 30 días
c. 40 días
d. 80 días

2. Los siguientes envases de lata tienen el mismo volumen.

a. ¿ cuál es la medida del radio del envase 1?
b. ¿ cuál es el envase que requiere menos material para su construcción?


3. Un auto sale de A hacia B a 120 km/h. En ese mismo instante, sale de B hacia A un camión a 90 km/h. Si se sabe que la distancia entre A y B es de 525 km, el tiempo que tardarán en encontrarse es de

a. 1,5 horas
b. 2 horas
c. 2,5 horas
d. 3 horas

4. La figura mostrada representa el movimiento de los autos A y B. Halle la distancia (en metros) que los separa en el instante t=9 seg.

a. 100 m
b. 85 m
c. 95 m
d. 80 m

CONTESTE LAS PREGUNTAS 5 Y 6 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN

La gráfica muestra la relación entre la posición de un cuerpo en función del tiempo

5. El desplazamiento total efectuado por el cuerpo, es

a.  0 cm

b. 10 cm

c.  20 cm

d.  30 cm

6. La distancia total recorrida por el cuerpo, es

a. 10 cm

b. 40 cm

c. 0 cm

d. 30 cm

CONTESTE LAS PREGUNTAS 7 Y 8 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN

El péndulo esquematizado en la figura oscila entre los puntos 1 y 2. El tiempo que tarda en ir del punto 1 al punto 2 es un segundo.

7. La frecuencia de oscilación del péndulo vale:
a. 0,5 Hz
b. 2 Hz
c. 1 Hz
d. 1,5 Hz

8. En el péndulo anterior, la cuerda de longitud L, se cambia por otra de longitud 4L. Comparando con la frecuencia de oscilación f, la nueva frecuencia es.
a. 2f
b. f/4
c. igual a f
d. f/2

CONTESTE LAS PREGUNTAS 9 Y 10 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN

Una niño deja caer periódicamente piedras sobre un punto de un estanque con agua. Después de 1 seg  observa que se han formado 15 frentes de onda y que la rapidez de avance de ellos es de 15 m/s.

9. 0,4 segundos después de haber arrojado la primera piedra la cantidad de frentes de ondas que observa es.

a. 5

b. 6

c. 7

d. 8

10. La longitud de onda de estas perturbaciones es igual a:

a. 10 m

b. 15 m

c. 2 m

d. 1m

CONTESTE LAS PREGUNTAS 11 A 13 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN
La siguiente gráfica de la posición (x) como función del tiempo de una esfera que se mueve sobre una linea recta.

                                  

11. De la gráfica se concluye que la longitud total recorrida por la esfera entre t=2,5 y 10 segundos es
a. 0,2 m
b. 0,5 m
c. 3 m
d. 0,3m

12. La posición de la esfera en t=10 segundo es
a. 0
b. 0,2 m
c. 0,1 m
d. 0,5 m

13. la frecuencia es
a. 0,1 Hz
b. 0,2 Hz
c. 0,3 Hz
d. 0,4 Hz

14. En el plano cartesiano se localizan tres punto P=(-4,-3), Q=(3,4) y R=(4,-3), luego se unieron formando el triángulo en de la figura. El área de dicho triángulo en unidades cuadradas es

a. 24 
b. 26
c. 28
d. 30

15. Se necesita transformar un lote de forma cuadrada en otro de forma rectangular, aumentando el largo en un 10% y disminuyendo el ancho en un 10%. De acuerdo a lo anterior, al realizar este proceso, el área del rectángulo con respecto al área del cuadrado inicial

  a. Disminuyó 1%

 b. Aumentó 1% 
 c. Disminuyó 10%
 d. Quedó igual

 16. Andrés quiere construir una escalera como la que se muestra en la figura, de esta manera podemos concluir que el volumen de concreto utilizado es de

 a.  0,72 metros cúbicos

 b.  0,072 metros cúbicos
 c.  0,96 metros cúbicos
 d.  0,48 metros cúbicos

17. La siguiente gráfica representa el movimiento de una partícula. 

La distancia recorrida por la partícula durante los primeros 2 seg es 
a. 15 m
b. 25 m
c. 45 m
d. 30 m

18. En el triángulo ABC, la suma del ángulo A y el ángulo B es 110 grados, y D es un punto sobre el segmento AB tal que CD=CB y el ángulo DCA es 10 grados. ¿Cuánto mide el ángulo A?

a. 40 grados

b. 45 grados

c. 30 grados

d. 50 grados

RESPONDA LAS PREGUNTAS 19 Y 20 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN

19. La caja en que tiene más probabilidad de sacar una bolita roja sin mirar es

a. La caja A
b. La caja B
c. La caja C
d. La caja D

20. Si se reúnen todas las bolitas de las cuatro cajas en una sola caja, la probabilidad de sacar una bolita de color blanco es

a. 1/2
b. 1/3
c. 1/4
d. 1/5

21. Una empresa embotelladora tiene un tanque esférico de agua mineral, cuya capacidad es de mil botellas. Si la empresa decide sustituir el tanque por otro que también es esférico pero cuyo diámetro es el triple del anterior; ¿Cuál sería la capacidad del nuevo tanque?
a. Tres mil botellas
b. Seis mil botellas 
c.  Nueve mil botellas 
d. Veintisiete mil botellas

22. La gráfica representa el movimiento de dos partículas A y B que viajan con aceleraciones aA y aB en linea recta. La relación entre aB y aA es:

a. 6
b. 5
c. 4
d. 3

RESPONDA LAS PREGUNTAS 23 Y 24 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN

La velocidad de una partícula con relación al tiempo se muestra en la gráfica

23. La distancia total recorrida por la partícula es 
a. 12 m
b. 25 m
c. 35 m
d. 45 m

24. El desplazamiento total es
a. 10 m
b. 5 m
c. 12 m
d. 15 m
RESPONDA LAS PREGUNTAS 25, 26 Y 27 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN
El movimiento de una moto de carreras se muestra en la siguiente gráfica de velocidad vs tiempo.

25. La aceleración de la moto en los primeros 3 segundos fue

26.  Cuál fue el desplazamiento de la moto entre t=0  y t=7 seg.

a. 30 m

b. 40 m

c. 50 m

d. 60 m

27.  La aceleración de la moto en t=4 seg fue

RESPONDA LAS PREGUNTAS 28, 29 Y 30 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN

Junior FC es un equipo de fútbol que participó en un campeonato de 20 equipos. Luego de que Junior FC jugó exactamente una vez contra cada uno de los otros equipos, obtuvo 43 puntos en total, se sabe además que perdió 2 partidos.

Aclaración: En un partido de fútbol, el equipo ganador recibe 3 puntos y el perdedor 0 puntos, y en caso de empate cada uno recibe 1 punto.

28.  Las ecuaciones que nos permiten hallar correctamente la cantidad de partidos ganados (G) y empatados (E) es.

a.  G+E=17

     3G+E=43
b.  2G+3E=17

           G+5E=43

      c.  -G+2E=17

           5G+E=43

      d.  7G-E=17

           2G+E=-43

   

     29. El número de partidos ganados fue

      a. 13

      b. 5

      c. 10

      d. 7

    30. El número de partidos empatados fue

      a. 5

      b. 13

      c. 7

      d. 4

    31. La gráfica muestra el movimiento de dos carros en linea recta. El tiempo en que los carros tienen la misma velocidad es
      

     a. 7,5 seg

     b. 8 seg

     c. 8,5 seg

     d. 9 seg

   

     32. con relación a la figura mostrada, el área de la región sombreada en centímetros cuadrados es

           

      a. 16-4pi

      b. 18-4pi

      c. 16-2pi

      d. 18-2pi

     33. El espacio ocupado por la siguiente figura, en unidades cubica es 

         

     
   a. 20

   b. 30

   c. 40

   d. 50

   

    RESPONDA LAS PREGUNTAS DE LA 34 A LA 37 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN

      Un estudiante de la especialidad de mecánica construye el siguiente mecanismo con dos   ruedas unidas por una banda, como lo indica la figura. Si el radio mayor es tres veces el radio menor.  

        

   34. La velocidad tangencial o lineal es

        a. Mayor en la rueda 1

        b. Mayor en la rueda 2

        c. No se puede calcular

        d. Igual en ambas ruedas

   35.  El periodo de la rueda 2 será
        a.  La tercera parte del periodo de la rueda 1
        b.  El triple del de la rueda 1
        c.   Igual al de la rueda 1
        d.   La mitad del de la rueda 1
   
   36. Si la frecuencia de la rueda 1 es 5 Hz, el periodo de la rueda 2 será 
        a. 15 seg 
        b.  5 seg
        c.  1/15 seg
        d.  1/5 seg
   
   37. Si el radio de la circunferencia pequeña es 5 cm y el periodo es de 4 seg, la velocidad angular en radianes por segundo, de la rueda grande es
      a. pi/6
      b. 3pi
      c. 6pi
      d. pi/2

    RESPONDA LAS PREGUNTAS 38 y 39 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN

      Una empresa petrolera utiliza barriles para enviar su producto al exterior. Si el barril tiene una base circular de 50 cm de diámetro y 80 cm de altura.

                                                             

    38. Cuál es su volumen, en centímetros cúbicos

          a. 20.000pi

          b. 25.000pi

          c. 45.000pi

          d. 50.000pi

    39. Cuanto material fue utilizado para la construcción de un barril, en centímetros cuadrados

          a. 5.250pi

          b. 4.250pi

          c. 6.240pi

          d. 7.250pi

    40. Si una esfera puede inscribirse perfectamente en un cilindro de diámetro 6 cm y altura 6 cm. El volumen de la esfera, en centímetros cúbicos, es:

       a. 46pi

       b. 14pi

       c. 10pi

       d. 36pi

    41. El volumen de un cilindro es 250pi. Si el radio de la base es la mitad del alto del cilindro. ¿Cuál es la altura del cilindro?

      a. 25

      b. 50

      c. 56

      d. 10

   

    42. Las coordenadas del único punto en común entre las rectas de ecuaciones 2Y+X=4 y 2Y-X=4 son

     a. (-2,0)

     b. (0,2)

     c. (2,0)

     d. (0,-2)

   43. La edad de Carlos es el doble de la edad de Maria e igual a la cuarta parte de la edad de Sebastian. Si la suma de las edades de Carlos, Maria y Sebastian es 22 años, ¿Qué edad tiene Carlos?

      a. 7 años

      b. 6 años

      c. 4 años

      d. 3años

   44. En la ilustración se muestra el plano de tres lotes contiguos E, F y G y algunas de las medidas de sus lados. La suma de las medidas de los frentes sobre la carrera segunda es 120 metros. Los segmentos resaltados en el plano son paralelos.

     

     Las medidas de los frentes de los lotes E, F y G sobre la carrera segunda son, respectivamente,

    a. 16 m, 41m y 25m

    b. 24m, 60m y 36m

    c. 24m, 64m y 32m

    d. 40m, 70m y 50m

    

    RESPONDA LAS PREGUNTAS DE LA 45 A LA 47 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN    

      La empresa de acueducto de un municipio cobra a sus suscriptores el consumo mensual de agua usando la siguiente función, C(n)=2n+3

      Donde C(n) está dado en miles de pesos y n es el consumo de metros cúbicos en un mes.

     45.  Si una familia consume 4 metros cúbicos en determinado mes, el costo que debe pagar es

      a.   $12.000

      b.   $11.000

      c.   $9.000

      d.   $8.000

        46. En el mes pasado, la familia Gómez hizo un pago a la empresa de acueducto por un valor de       $23.000. De acuerdo con esto, la cantidad de metros cúbicos consumidos por la familia Gómez es de

       a.  10

       b.  11

       c.   12

       d.  13

     47.  Si en una casa desocupada no hay consumo durante un mes, el valor que debe cancelar el dueño          de esta casa a la empresa de acueducto es

       a.  $3

       b.  $5

       c.  $3.000

       d. $5.000

              RESPONDA LAS PREGUNTAS 48 Y 49 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN

       Carlos manda a construir un estanque en su patio, en la figura se muestra la vista superior de dicho estanque el cual está formado por un cuadrado y dos semicírculos a los lados.

      

    48. Si Carlos decide cubrir el estanque por las noches para evitar que se llene de hojas. La cantidad aproximada en metros cuadrados de tela a utilizar es 
     a. 7,14
     b. 8
     c. 8,14
     d. 11,14

49. Si un gusano que mide 4cm de longitud da una vuelta completa por el borde alrededor del estanque, entonces este recorre aproximadamente
    a. 154 veces su longitud
    b. 257 veces su longitud
    c. 414 veces su longitud
    d. 600 veces su longitud
   

   50. Carlos construye un árbol de navidad el cual tiene forma de triángulo isósceles con altura de 200 cm y está decorado en la parte superior por una estrella dorada, como se muestra en la figura.

   

      Si los ángulos de la base miden ambos 60 grados, entonces la medida de la base (b) del árbol, en centímetros es

     

  

   51. Se debe construir un gráfico circular que indique la cantidad de veces que se han comprado 5 productos en una tienda. ¿Cuántos grados del gráfico circular les corresponden a las papas?

     

  

    a. 12 grados

    b. 60 grados

    c. 120 grados

    d. 150 gados 

   52. En un grupo de 200 personas el 30% habla ingles, el 50% habla español y el 10% habla los dos idiomas. Los que no hablan ninguno de los dos idiomas son.

   a. 20 personas

   b. 60 personas

   c. 30 personas

   d. 40 personas

    RESPONDA LAS PREGUNTAS DE LA 53 A LA 55 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN  

     El siguiente gráfico de posición contra tiempo, representa el movimiento de una partícula durante 10 segundos. Basándose en la información que éste suministra, responda.

     

    53. La distancia recorrida por la partícula entre t=0 y t=10 segundos es:

    a. 80 m

    b. 60 m

    c. 30 m

    d. 40 m

    54. El desplazamiento total de la partícula es: 

    a. nulo

    b. 50 m

    c. 40 m

    d. 80 m

   

    55. Entre t=2 seg y t=4 seg, podemos decir que la partícula.

    a. No se ha movido

    b. Se movió a la derecha

    c. Recorrió 20 m

    d. Vuelve a donde salió

    

   56. Cada 15 días, Santiago corta el pasto de las orillas de su jardín que tiene forma cuadrada. El resto del jardín permanece intacto para que sirva como hábitat de pájaros. El terreno mide b metros por b metros y la franja podada es de x metros de ancho.

     

    El área de la parte podada es
    a. 4x(b-x)
    b. 4xb
    c. 4x
    d. 4(x+b)

   57. El dibujo muestra la posición inicial de dos autos que tienen velocidad constante. ¿Qué distancias estarán separados al cabo de 4 horas?
   

    a. 49 km

    b. 50 km

    c. 39 km

    d. 60 km

   58.  Dos esferas metálicas cargadas eléctricamente penden de hilos no conductores como se ilustra en la figura.

      

    De los siguientes, la figura que ilustra las fuerzas eléctricas sobre las esferas cuando se acercan la una

    a la otra es

    

  

   59. En la figura aparecen dos circunferencias tangentes entre sí y tangentes a una recta. Si el radio de las circunferencias es r, entonces el área de la región sombreada es 

     

   

  

    RESPONDA LAS PREGUNTAS 60 Y 61 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN

       En un triángulo rectángulo se tiene que su hipotenusa mide 10 cm y uno de los catetos mide el triple del otro.

     

    60. Podemos decir que las medidas de los catetos son

    

   

   61. El área del triángulo es

    

   

   62. De una hoja de papel Sara recorta un triángulo rectángulo como se muestra:

         

    Después decide recortar un círculo y le sobran 3(20-3pi) centímetros cuadrados de papel. ¿El radio del circulo cortado es?

   

    a. 9 cm

    b. 6 cm

    c. 3 cm

    d. 2 cm

    63. La gráfica representa varios movimientos parabólicos. Si cada uno de los movimientos sale con la misma velocidad se puede deducir que

     

   a.  A mayor ángulo su alcance es mayor

   b.  A menor ángulo su altura es mayor

   c. Cuando los ángulos son suplementarios caen en el mismo lugar

   d. Cuando los ángulos son complementarios caen en el mismo lugar

    64. En la gráfica adjunta, la altura (h) de la montaña y el valor de (x) son respectivamente:

         

    

   

    65. Cuando María camina de A hasta B 40 metros hacia el edificio; el ángulo de elevación crece de 30 a 60 grados. La altura del edificio es:

      

   

   

     RESPONDA LAS PREGUNTAS 66 AL 68 TENIENDO EN CUENTA LA SIGUIENTE INFORMACIÓN.

     Un automóvil se mueve con un movimiento rectilíneo uniforme, y recorre una distancia de 200 metros en 20 segundos. 

     

                                                         

       66. Se puede asegurar que en el quinto segundo el auto lleva una velocidad de

     

  

    67. En el quinto segundo el auto ha recorrido una distancia de

         A.    50 m

         B.     40 m

         C.     30 m

         D.    20 m

    68. La aceleración en el quinto segundo es

     

   69. 

      70. La ecuación de la recta, que pasa por el punto (3, -2) y es perpendicular a la recta de ecuación Y=2X - 9, es
        
       71. En un triángulo rectángulo, uno de los catetos mide 6 cm. Si la hipotenusa mide x, el valor del otro cateto es:
   

      

      72. Sabiendo que "C" es la medida de un cateto, ¿Cuál es el valor de la hipotenusa del triángulo rectángulo si el otro cateto mide la mitad del ya mencionado? 

    

     74. Para el triángulo rectángulo mostrado, podemos decir que las medidas de sus lados       son:

     

     a. (13, 10, 8)

     b. (20, 10, 5)

     c. (13, 12, 5)

     d. (20, 12, 7)

    

    

     

   

      
    

 84. La probabilidad de que ocurra un evento específico como resultado de un experimento aleatorio es un  número comprendido entre 0 y 1. Se le asigna 0 si el evento es imposible y 1 si el evento con seguridad ocurre.
    Al lanzar un dado sobre una mesa la probabilidad de que, en la cara superior, salga un número par mayor que 3 es.
      A. 1/3
      B. 1/6
      C. 2/3
      D. 3/2

     85. Si lanzamos al aire un dado, se puede afirmar que la probabilidad de que caiga en un número

           A. par, es menor a la probabilidad de que caiga un número impar.

           B. múltiplo de 3, es menor a la probabilidad de que caiga un múltiplo de 4.

           C. par, es igual a la probabilidad de que caiga un número menor que 4.

           D. divisor de 5, es mayor a la probabilidad de que caiga un divisor de 6.

    86. Las pantallas de los aparatos tecnológicos se venden según la longitud de la linea diagonal, como  se muestra en la siguiente figura.

         

   Si se necesita comprar una pantalla para una tableta de 15 pulgadas, las dimensiones que esta debe tener es de:
       

    87. Para el almacenamiento de agua se dispone de dos tanques, con las dimensiones que se indican en el dibujo.

   De acuerdo con la dimensión de los recipientes, se puede afirmar que el volumen del tanque

    A. 1 es la mitad del volumen del tanque 2.

    B. 1 es igual al volumen del tanque 2.

    C. 2 es el triple del volumen del tanque 1.

    D. 2 es la mitad del volumen del tanque 1.

   88. Juan colocó una extensión de luces de 17 metros desde la base de su casa hasta la cima de un poste de 15 metros, como se muestra a continuación.

   

   A partir de la información anterior se puede afirmar que la distancia más corta entre el poste y la casa es de
   A. 2 metros
   B. 4 metros
   C. 6 metros
   D. 8 metros

    RESPONDA LAS PREGUNTAS 89 Y 90 DE ACUERDO CON LA SIGUIENTE INFORMACIÓN 

   Un movimiento armónico simple, es un movimiento periódico en el que la posición varia según una ecuación de tipo senoidal o cosenoidal.

   Si una partícula describe un movimiento representado por la gráfica mostrada.

   89. La amplitud de este movimiento es

         A. 6 metros

         B. 5 seg

         C. 3 metros

         D. 10 seg

   90. El periodo de este movimiento es

         A. 5 seg

         B. 4 seg

         C. 6 metros

         D. 10 seg

    

   91. Si un litro equivale a 1 decímetro cubico; el número de litros que caben en un cubo de 40 centímetros de arista es:

       A. 64

       B. 40

       C. 16

       D. 50

  

   92. La ecuación de la recta que pasa por el punto (-2, 3) y es perpendicular a la recta 3X+2Y-8=0 es

        A. 2X-3Y-13=0

        B. 2X-3Y+13=0

        C. 2X+3Y+13=0

        D. 3X-2Y+13=0

  93. Los 4/5 de una suma de dinero colocadas al 3% mensual durante 2 meses producen $1.200 de intereses. La suma de dinero es:
      A. $25.000
      B. $24.000
      C. $23.000
      D. $20.000